This is the home page for the kinetic Monte Carlo code SPPARKS, an acronym for Stochastic Parallel PARticle Kinetic Simulator.

SPPARKS is a parallel Monte Carlo code for on-lattice and off-lattice models that includes algorithms for kinetic Monte Carlo (KMC), rejection kinetic Monte Carlo (rKMC), and Metropolis Monte Carlo (MMC). It implements several KMC solvers whose serial computational complexity ranges from O(N) to O(NlogN) to O(1) in the number of events N owned by a processor. In a generic sense the solvers catalog a list of "events", each with an associated probability, choose a single event to perform, and advance time by the correct amount. Events may be chosen individually at random, or by sweeping over sites in a more ordered fashion.

Applications that are packaged with SPPARKS, or which a user adds to the code, define sites and events and probabilities, as well as how the execution of an event changes the state of the model.

SPPARKS runs on single processors or in parallel using message-passing techniques and a spatial-decomposition of the simulation domain. The code is designed to be easy to modify or extend with new functionality.

SPPARKS is distributed as an open source code under the terms of the GPL, or sometimes by request under the terms of the GNU Lesser General Public License (LGPL). The current version can be downloaded here.

SPPARKS was developed at Sandia National Laboratories, a US Department of Energy laboratory. The Authors page lists the developers and their contact info, along with others who have contributed code to SPPARKS. Funding for SPPARKS development has come from the DOE and is also acknowledged on the Authors page.

• (11/24) New potts/quaternion application to include relative lattice orientation differences between sites in the Hamiltonian energy function which drives grain growth and texturing. See the description of the 27Nov24 release on this page.
• (9/23) New potts/am/bezier application for modeing additive manufacturing of metals, using Bezier curves to fit the meltpool shape. See the description of the 6Sep23 release on this page.
• (6/22) New diffusion/multiphase application which allows any number of different phases (atomic species for an atomic-scale model) to be used, any of which can be immobile (pinned) or mobile (diffusing). See the description of the 24Jun21 release on this page.
• (7/20) A variety of options were added for modeling additive manufacturing processes via Potts model simulations which evolve microstructure in the presence of a moving laser spot which heats material. See the description of the 23Jul20 release on this page.
• (7/20) A new I/O system called the Stitch library has been added to SPPARKS. It was specially developed for additive manufacturing (AM) simulations. Using Stitch, an output database for microstructure simulations is created incrementally by appending lattice sites much in the same way new material is added to an AM part. See the dump stitch and set stitch commands for details, as well as the stitch and am_path folders in the examples directory.
• (11/16) A variety of new input/output options were added, including dump sites and dump vtk styles, and dump_modify and read_sites options. These make it easier to use SPPARKS with VTK-compatible visualizers, like ParaView, and to continue/restart SPPARKS simulations using dump file snapshots as a restart file.
• (3/12) Release of Python wrapper for SPPARKS in python dir with additional examples of using SPPARKS as a library in the example/COUPLE dir.
• (11/09) Release of 11 Nov 2009 version of SPPARKS. New commands and features include: app_style diffusion, app_style relax, barrier, create_box, create_sites, deposition, diag_style propensity, dimension, dump_modify, dump_one, lattice pair_coeff, pair_style, processors, read_sites, region, set, undump, and Schwoebel hops via the app_style diffusion command. See details here.
• (9/09) First off-lattice parallel application added.
• (4/09) Initial open-source release of SPPARKS.

This is work by Liz Holm (eaholm at sandia.gov) at Sandia and Todd Hoffmann (todd.hoffmann at asu.edu) and his advisor at Carnegie Mellon, to study the mechanisms and statistics associated with abnormal grain growth. In grain growth, when the system is annealed, grain boundaries will move and rearrange so as to increase the average grain size and decrease the grain boundary area per unit volume. In normal grain growth, this occurs relatively uniformly, but in abnormal grain growth, one grain grows at the expense of the others. Abnormal grain growth can have many causes. Here the effects of static particle dispersions on grain growth are studied. Particles should pin grain boundaries in positions that maximize their contact with the particles, so that grain growth cannot proceed. However, occasionally one grain breaks free and is able to grow at the expense of others, leading to abnormal growth.

The images and movies show typical results for a 300x300x300 lattice, run for a million Monte Carlo steps (sweep over all lattice sites), with 5 volume percent pinning particles, inserted when the average grain radius was 10 sites. In the normal case, the system becomes fully pinned. In the second case, abnormal growth eventually occurs.

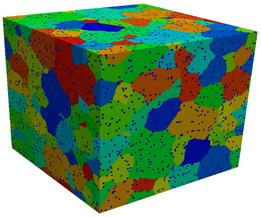
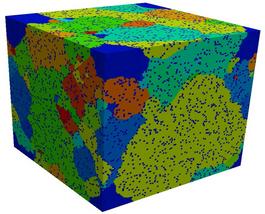
Two images and two 1.5 Mb AVI movies