Potts model context¶

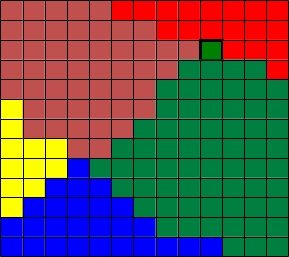
• Digitize space (lattice)

  • Lattice sites represent discrete bits of material

  • Each color represents membership in a phase/grain

    

• Potts algorithm seeks to minimize the total energy

• Total grain boundary energy: \(E\)

  \[\begin{split}E=\sum_i^N \; \sum_j^nJ(1-\delta_{ij}) \\\end{split}\]

  \(N\) – number of sites; \(n\) – number of neighboring sites; \(J\) – bond energy

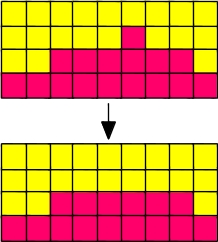
• Local energy consideration: \(\Delta E=-2,\;\; r=1.0\) (see below)

  

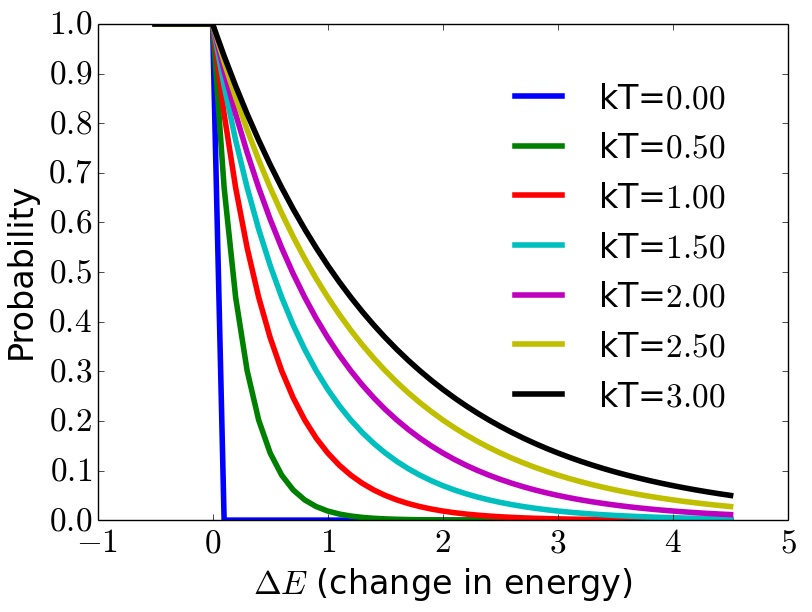
• Rates \(r\) computed to mimic atomic processes – Boltzmann distribution

  \[\begin{split}r=\begin{cases} 1 & \Delta E\leq 0\\ e^{-\frac{\Delta E}{kT}} & \Delta E > 0 \end{cases}\end{split}\]
  • Events that decrease energy have higher rates